Kobon Triangle -- from Wolfram MathWorld
4.7 (704) · $ 10.00 · In stock
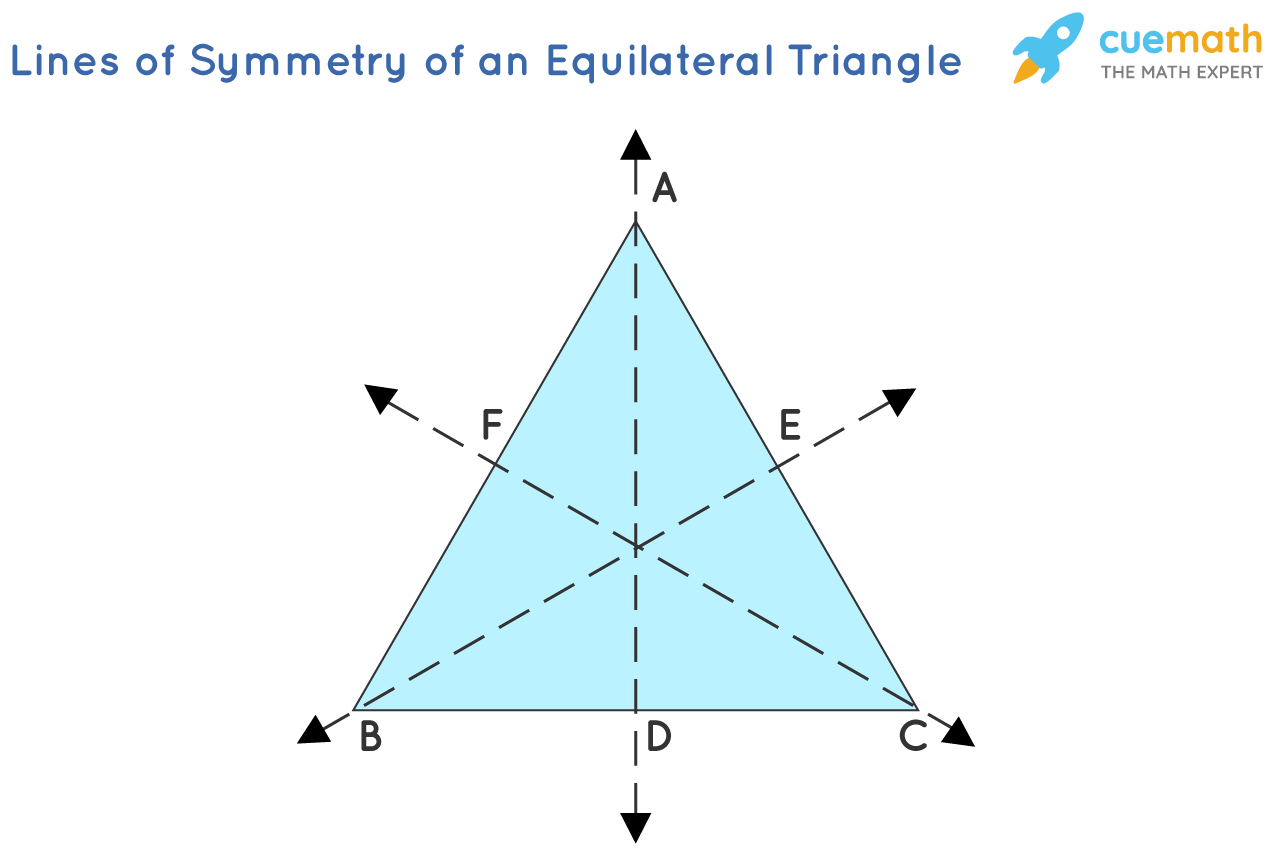
Kobon Fujimura asked for the largest number N(n) of nonoverlapping triangles that can be constructed using n lines (Gardner 1983, p. 170). A Kobon triangle is therefore defined as one of the triangles constructed in such a way. The first few terms are 1, 2, 5, 7, 11, 15, 21, (OEIS A006066). It appears to be very difficult to find an analytic expression for the nth term, although Saburo Tamura has proved an upper bound on N(n) of |_n(n-2)/3_|, where |_x_| is the floor function (Eppstein).

Kobon Triangle -- from Wolfram MathWorld

Cleaver -- from Wolfram MathWorld


Obtuse Triangle -- from Wolfram MathWorld
Kobon triangle problem - Wikipedia

MEDIAN Don Steward mathematics teaching: Kobon triangles

Triangle Counting -- from Wolfram MathWorld

Altitude -- from Wolfram MathWorld

Steiner Triangle -- from Wolfram MathWorld
IGS, Dynamic Geometry 1459: Two Triangles, Orthocenter, Midpoint, Perpendicular, Step-by-step Illustration, GeoGebra, iPad Apps. Typography